Linear SHM

A horizontal cylinder closed at one end contains an ideal gas which is compressed by a tight-fitting and frictionless piston. The piston is connected to the other closed end of the cylinder via a spring with spring constant $k$. The piston is of cross-sectional area $A$ and mass $M$. In equilibrium, the chamber containing the gas has pressure $P$ and length $L$ while the spring is compressed by $l$. Let the the piston be displaced by $d(\ll L)$ towards the vacuum region, and released. Choose the correct statement(s) regarding the oscillations of the piston by assuming all processes are isothermal.

If $\text{'}\mathrm{x}\text{'}$ is the displacement of a particle performing SHM, then $"\raisebox{1ex}{${\mathrm{kx}}^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right."$ is equal to its _________ energy.

The K.E of a particle performing simple harmonic motion is _______ whose displacement is $\mathrm{f}\left(\mathrm{t}\right)=\mathrm{A} \cos \left(\mathrm{\omega t}+\mathrm{\varphi }\right)$.

The kinetic energy and potential energy of a particle exerting simple harmonic motion of amplitude $\text{'}\mathrm{A}\text{'}$ will be equal when displacement is

For a body executing SHM, its potential energy for displacements $\mathrm{a}$and $\mathrm{b}$ are ${\mathrm{E}}_{\mathrm{a}}$ and ${\mathrm{E}}_{\mathrm{b}}$ respectively. Then what is the potential energy $\mathrm{E}$ at a displacement ${\left(\mathrm{a}+\mathrm{b}\right)}^2$.

Plot the graph of potential energy versus time for a pendulum performing the simple harmonic motion.

Graph of kinetic energy in terms of displacement in SHM :-

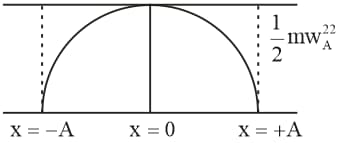
 At displacement $x=$_____ of a particle executing SHM, has maximum kinetic energy.

A mass $\mathrm{m}$ is suspended one by one by two springs of force constants ${\mathrm{k}}_1, {\mathrm{k}}_2$. The time periods of their oscillations are ${\mathrm{T}}_1 \mathrm{and} {\mathrm{T}}_2$ respectively. If the same mass be suspended by connecting the two springs in parallel then the time period of oscillations is $\mathrm{T}$.The correct relation is:

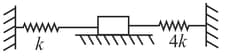
A solid block on a frictionless surface is connected to two rigid supports on the left and right side by springs of spring constants $k$ and $4k$ respectively as shown in the figure. The time spent by the block in a complete cycle of oscillation on the left and the right side of the equilibrium position are $t_L$ and $t_R$ respectively. Which of the following is correct?

If a watch with a wound spring is taken on to the moon. It

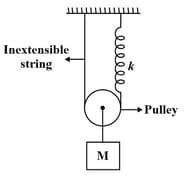
The time period for small vertical oscillations of a block of mass $\mathrm{m}$ when the masses of the pulleys are negligible and spring constant ${\mathrm{k}}_1$ and ${\mathrm{k}}_2$ is

An arrangement of spring, strings, pulley and masses is shown in the figure below.

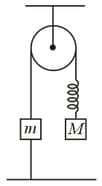
The pulley and the strings are massless and $M>m$. The spring is light with spring constant $k$. If the string connecting $m$ to the ground is detached, then immediately after detachment

A force constant of ideal spring is $200 \mathrm{N} {\mathrm{m}}^{-1}$. It is loaded with a mass $\frac{200}{{\pi }^2} \mathrm{kg}$ at the lower end the period of its vibration is:

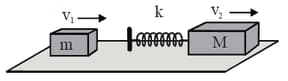
Two blocks of masses $m$ and $M$ are moving with speed $v_1$ and $v_2\left(v_1>v_2\right)$ in the same direction on the frictionless surface respectively, $M$ being ahead of $m$. An ideal spring of force constant $k$ is attached to the backside of $M$ (as shown). The maximum compression of the spring when the blocks collide is 

A mass $m$ is suspended from a weightless spring and it has time-period $T$. The spring is now divided into four equal parts and the same mass is suspended from one of these parts. The now time period will be:-

Angular frequency in SHM is given by $\text{ω}=\sqrt{\frac{\text{k}}{\text{m}}}$. Maximum acceleration in SHM is ${\text{ω}}^{2}A$ and maximum value of friction between two bodies in contact is $\text{μ}\text{N}$, where N is the normal reaction between the bodies.
  Now the value of k, the force constant is increased, then the maximum amplitude calculated in above question will

Electrostatic force on a charged particle is given by $\overrightarrow{\text{F}}=\text{q}\overrightarrow{\text{E}}$. If q is positive $\overrightarrow{\text{F}}\uparrow \uparrow \overrightarrow{\text{E}}$ and if q negative $\overrightarrow{\text{F}}\uparrow \downarrow \overrightarrow{\text{E}}$

In the figure m_A = m_B = 1 kg. Block A is neutral while q_B = - 1C. Sizes of A and B are negligible. B is released from rest at a distance 1.8 m from A. Initially  spring is neither compressed nor elongated.

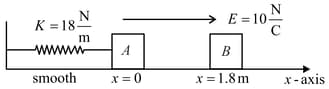
Equilibrium position of the combined mass is at $x = ........m$

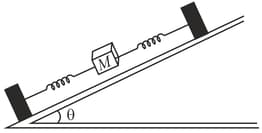
A body of mass $M$ is attached between two massless springs of force constant $K$ on a smooth plane of inclination $\mathrm{\theta }$. The other ends of the springs are fixed to vertical walls. The time period of oscillation of the body will be

Statement 1: Acceleration must be proportional to displacement and directed towards mean position in a simple harmonic motion.

Statement 2: A mass $\mathrm{M}$ is suspended from vertical spring of some force constant and the equation of motion is $\mathrm{My}=-\mathrm{ky}+\mathrm{Mg}$as shown in the Figure, then it shows that motion is not simple harmonic unless $\mathrm{Mg}$ is negligibly small.

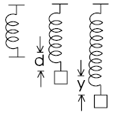
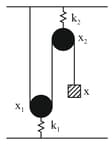
The time period of mass $M$ when displaced from its equilibrium position and then released for the system as shown in figure is